۸
مهر

جلسه ۲۲ : حل معادلات دیفرانسیل در متلب

دسته‌بندی‌ها :

جزئیات
نوع محتواآموزش تصویری

فهرست

مقدمه

با عرض سلام و وقت بخیر خدمت کاربران سایت پی وی لرن. و کاربرانی که دوره کامل آموزش متلب را دنبال می کنند. متلب به عنوان یک نرم افزار مهندسی و محاسباتی قدرتمند، توابع گسترده ای را برای حل انواع معادلات درجه ۲ ، ۳، ۴ و بالاتر را به شما ارائه می دهد. یکی از قابلیت های محاسباتی پرکاربرد در متلب ، قابلیت حل انواع معادلات دیفرانسیل و لگاریتمی و همچنین رسم نمودارهای توابع لگاریتم می باشد. در ادامه مباحث آموزش حل معادلات دیفرانسیل در متلب شما را با چگونگی حل انواع معادلات و توابع لگاریتم آشنا می کنیم.

حل معادلات دیفرانسیل در متلب

MATLAB دستور diff را برای محاسبات دیفرانسیل در اختیار شما قرار می دهد.

در ساده ترین حالت عبارت دیفرانسیل را در متغیری قرار داده و آن در تابع diff محاسبه می کنیم.

برای مثال ما دیفرانسیل تابع f(t) = 3t² + ۲t^-2 را محاسبه می کنیم.

مثال – یک فایل اسکریپت ایجاد کرده و کدهای زیر را در آن قرار می دهیم:

مثال :

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

syms t

f = 3*t^2 + 2*t^(-2);

diff(f)

نتیجه ی اجرای کد فوق در متلب بصورت زیر خواهد بود:

مثال :

ans =
6*t - 4/t^3

1 2	ans = 6*t - 4/t^3

حال کدهای فوق را در Octave بررسی می کنیم:

مثال :

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

t = sym("t");

f = 3*t^2 + 2*t^(-2);

differentiate(f,t)

نتیجع ی اجرای کد فوق در Octave بصورت زیر است:

مثال :

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

1 2	ans = -(4.0)t^(-3.0)+(6.0)t

تایید قوانین ابتدایی تمایز

بگذارید خلاصه ای از معادلات و مقررات مختلفی برای تمایز توابع استفاده کنیم قوانین آن ها را بررسی کنیم.

قانون ۱

برای هر توابع f و g و هر عدد حقیقی a و b مشتق تابع هستند.

(h(x) = af(x) + bg(x
(h'(x) = af'(x) + bg'(x

قانون ۲

قوانین sum و subtraction (جمع و تفریق) بیان می کنند که اگر f و g دو توابع باشند، f ‘و g’ به ترتیب مشتقات آنها هستند.

f + g)’ = f’ + g’)
f – g)’ = f’ – g’)

قانون ۳

قانون product بیان می کند که اگر f و g دو توابع باشند، f ‘و g’ به ترتیب مشتقات آنها هستند.

f.g)’ = f’.g + g’.f)

قانون ۴

قانون quotient بیان می کند که اگر f و g دو توابع باشند، f ‘و g’ به ترتیب مشتقات آنها هستند.

f/g)’ = (f’.g – g’.f)/g²)

قانون ۵

قانون polynomial بیان می کند که برای تابع y = f(x) = xⁿمشتق آن تابع (f’ = n. x^(n-1 است.

یک نتیجه مستقیم از این قاعده این است که مشتق هر ثابت صفر است.

به عنوان مثال، اگر y = k، باشد سپس f ‘= 0 را خواهیم داشت.

قانون ۶

قانون chain بیان می کند که مشتق تابع (( h (x) = f (g (x با توجه به x است:

(h ‘(x) = f’ (g (x)) g ‘(x

مثال – یک فایل اسکریپتی ایجاد کرده و کد زیر را در آن قرار می دهیم:

مثال :

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

syms x

syms t

f = (x + 2)*(x^2 + 3)

der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)

der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)

der4 = diff(f)

f = (x^2 + 1)^17

der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)

der6 = diff(f)

زمانیکه فایل فوق را اجرا کنید، نتیجه ی زیر را مشاهده خواهید کرد:

مثال :

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

f =

(x^2 + 3)*(x + 2)

der1 =

2*x*(x + 2) + x^2 + 3

f =

(t^(1/2) + t^3)*(t^2 + 3)

der2 =

(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)

f =

(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 =

(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)

f =

(2*x^2 + 3*x)/(x^3 + 1)

der4 =

(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2

f =

(x^2 + 1)^17

der5 =

34*x*(x^2 + 1)^16

f =

1/(t^3 + 3*t^2 + 5*t - 9)^6

der6 =

-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

کد فوق در Octave بصورت زیر خواهد بود:

مثال :

x = sym("x");
t = sym("t");

f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 

f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 

f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 

f = (x^2 + 1)^17 
der5 = differentiate(f,x) 

f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

x = sym("x");

t = sym("t");

f = (x + 2)*(x^2 + 3)

der1 = differentiate(f,x)

f = (t^2 + 3)*(t^(1/2) + t^3)

der2 = differentiate(f,t)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 = differentiate(f,x)

f = (2*x^2 + 3*x)/(x^3 + 1)

der4 = differentiate(f,x)

f = (x^2 + 1)^17

der5 = differentiate(f,x)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)

der6 = differentiate(f,t)

نتیجه ی اجرای کد فوق در Octave:

مثال :

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

f =

(2.0+x)*(3.0+x^(2.0))

der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x

f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))

der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))

f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))

der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)

f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)

der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)

f =

(1.0+x^(2.0))^(17.0)

der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x

f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)

der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

مشتقات توابع نمایشی، لگاریتمی و مثلثاتی

جدول زیر مشتقات توابع معمولی، لگاریتمی و مثلثاتی را ارائه می دهد:

تابع	مشتق توابع
c^a.x	(c^a.x.ln c.a (ln is natural logarithm
e^x	e^x
ln x	۱/x
ln_cx	۱/x.ln c
x^x	(x^x.(1 + ln x
(sin(x	(cos(x
(cos(x	(-sin(x
(tan(x	(sec²(x), or 1/cos²(x), or 1 + tan²(x
(cot(x	((-csc²(x), or -1/sin²(x), or -(1 + cot²(x
(sec(x	(sec(x).tan(x
(csc(x	(-csc(x).cot(x

مثال – یک فایل اسکریپت ایجاد کرده و کد زیر را در آن قرار دهید:

مثال :

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

syms x

y = exp(x)

diff(y)

y = x^9

diff(y)

y = sin(x)

diff(y)

y = tan(x)

diff(y)

y = cos(x)

diff(y)

y = log(x)

diff(y)

y = log10(x)

diff(y)

y = sin(x)^2

diff(y)

y = cos(3*x^2 + 2*x + 1)

diff(y)

y = exp(x)/sin(x)

diff(y)

نتیجه ی اجرای کد فوق در متلب بصورت زیر خواهد بود:

مثال :

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

y =

exp(x)

ans =

exp(x)

y =

x^9

ans =

9*x^8

y =

sin(x)

ans =

cos(x)

y =

tan(x)

ans =

tan(x)^2 + 1

y =

cos(x)

ans =

-sin(x)

y =

log(x)

ans =

1/x

y =

log(x)/log(10)

ans =

1/(x*log(10))

y =

sin(x)^2

ans =

2*cos(x)*sin(x)

y =

cos(3*x^2 + 2*x + 1)

ans =

-sin(3*x^2 + 2*x + 1)*(6*x + 2)

y =

exp(x)/sin(x)

ans =

exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

حالا کد فوق را در Octave پیاده سازی می کنیم:

مثال :

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

x = sym("x");

y = Exp(x)

differentiate(y,x)

y = x^9

differentiate(y,x)

y = Sin(x)

differentiate(y,x)

y = Tan(x)

differentiate(y,x)

y = Cos(x)

differentiate(y,x)

y = Log(x)

differentiate(y,x)

% symbolic packages does not have this support

%y = Log10(x)

%differentiate(y,x)

y = Sin(x)^2

differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)

differentiate(y,x)

y = Exp(x)/Sin(x)

differentiate(y,x)

نتیجه ی اجرای کد فوق بصورت زیر خواهد بود:

مثال :

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

y =

exp(x)

ans =

exp(x)

y =

x^(9.0)

ans =

(9.0)*x^(8.0)

y =

sin(x)

ans =

cos(x)

y =

tan(x)

ans =

1+tan(x)^2

y =

cos(x)

ans =

-sin(x)

y =

log(x)

ans =

x^(-1)

y =

sin(x)^(2.0)

ans =

(2.0)*sin(x)*cos(x)

y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))

ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))

y =

sin(x)^(-1)*exp(x)

ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

محاسبه مشتقات مرتبه بالاتر

برای محاسبه ی مشتقات درجه بالاتر از ساختار (diff(f,n استفاده می کنیم.

بگذارید مشتق دوم تابع y = f (x) = x .e-3x را محاسبه کنیم.

مثال :

f = x*exp(-3*x);
diff(f, 2)

1 2	f = xexp(-3x); diff(f, 2)

نتیجه ی اجرای کد فوق در متلب بصورت زیر خواهد بود:

مثال :

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

1 2	ans = 9xexp(-3x) - 6exp(-3*x)

همین کدها را در Octave قرار می دهیم:

مثال :

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

x = sym("x");

f = x*Exp(-3*x);

differentiate(f, x, 2)

نتیجه ی اجرای کد فوق در Octave:

مثال :

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

مثال – برای نمونه تابع (y = f(x) = 3 sin(x) + 7 cos(5x را در نظر می گیریم.

سپس می خواهیم صحت (f” + f = -5cos(2x را بررسی کنیم.

یک فایل اسکریپت ایجاد کرده و کد زیر را در آن قرار دهید:

مثال :

y = 3*sin(x)+7*cos(5*x);
lhs = diff(y,2)+y; 
rhs = -5*cos(2*x);
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

y = 3*sin(x)+7*cos(5*x);

lhs = diff(y,2)+y;

rhs = -5*cos(2*x);

if(isequal(lhs,rhs))

disp('Yes, the equation holds true');

else

disp('No, the equation does not hold true');

end

disp('Value of LHS is: '), disp(lhs);

سپس نتیجه ی زیر را در اجرا مشاهده خواهید کرد:

مثال :

Value of LHS is: 
-168*cos(5*x)

1 2	Value of LHS is: -168cos(5x)

حال این کدها را در Octave نیز بررسی می کنیم:

مثال :

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);          lhs = differentiate(y, x, 2) + y; 
rhs = -5*Cos(2*x);             

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

x = sym("x");

y = 3*Sin(x)+7*Cos(5*x); lhs = differentiate(y, x, 2) + y;

rhs = -5*Cos(2*x);

if(lhs == rhs)

disp('Yes, the equation holds true');

else

disp('No, the equation does not hold true');

end

disp('Value of LHS is: '), disp(lhs);

نتیجه ی اجرای کد فوق در Octave:

مثال :

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

No, the equation does not hold true

Value of LHS is:

-(168.0)*cos((5.0)*x)

یافتن حداکثر و حداقل یک منحنی

اگر ما برای حداکثر و حداقل برای حداکثر برای یک گراف جستجو می کنیم، اساسا به دنبال بالاترین یا پایین ترین نقاط در گراف تابع در یک مکان خاص هستیم.

برای یک تابع (y = f (x نقاط در نمودار که در آن گراف دارای شیب صفر است، نقاط ثابت است.

به عبارت دیگر نقاط ثابت، جایی است که f ‘(x) = 0 است.

برای پیدا کردن نقاط ثابت یک تابع که تمایز می دهیم، باید مشتق را برابر با صفر قرار دهیم و معادله را حل کنیم.

مثال – می خواهیم نقاط ثابت را برای تابع f(x) = 2x³ + ۳x² − ۱۲x + 17 بدست آوریم.

ابتدا به تابع وارد شویم و نمودار آن را طرح می کنیم.

مثال :

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; 
ezplot(y)

syms x

y = 2*x^3 + 3*x^2 - 12*x + 17;

ezplot(y)

MATLAB کد فوق را اجرا می کند و طرح زیر را برمی گرداند :

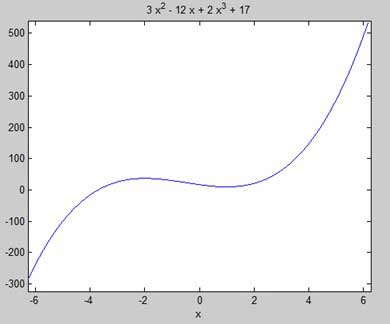
نتیجه ی اجرا کد رسم

حالا این کد را در Octave پیاده سازی می کنیم:

مثال :

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

x = sym('x');

y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)

print -deps graph.eps

هدف ما یافتن معادلات و مینیمم های محلی بر روی نمودار است.

بنابراین ما ماکزیمم ها و حداقل ها را برای فاصله [-۲، ۲] در نمودار پیدا می کنیم.

مثال :

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;
ezplot(y, [-2, 2])

syms x

y = 2*x^3 + 3*x^2 - 12*x + 17;

ezplot(y, [-2, 2])

نتیجه ی اجرای کد فوق در متلب بصورت زیر خواهد بود:

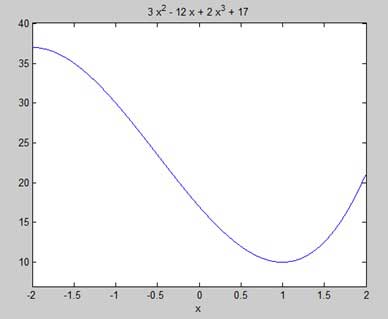
حالا این کدها را در Octave بررسی می کنیم:

مثال :

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

x = sym('x');

y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])

print -deps graph.eps

حال دیفرانسیل را محاسبه می کنیم:

مثال :

g = diff(y)

1	g = diff(y)

نتیجه ی اجرای کد فوق در متلب:

مثال :

g =
   6*x^2 + 6*x - 12

1 2	g = 6x^2 + 6x - 12

کدهای فوق در Octave بصورت زیر خواهد بود:

مثال :

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;

g = differentiate(y,x)

نتیجه ی اجرای کدهای فوق در Octave:

مثال :

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

1 2	g = -12.0+(6.0)x+(6.0)x^(2.0)

حالا تابع g را برای به دست آوردن مقادیری که آن صفر می شود، را حل می کنیم:

مثال :

s = solve(g)

1	s = solve(g)

نتیجه ی اجرای کد فوق در متلب:

مثال :

s =
   1
   -2

s =

-2

حالا همین کدها را در Octave پیاده سازی می کنیم:

مثال :

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;

g = differentiate(y,x)

roots([6, 6, -12])

نیتجه ی اجرای کدهای فوق در Octave:

مثال :

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x

ans =

-2

با استفاده از فرمان زیر می توان یک مقدار را در یک تابع نمادین جایگزین کرد:

مثال :

subs(y, 1), subs(y, -2)

1	subs(y, 1), subs(y, -2)

نتیجه ی اجرای کد فوق در متلب:

مثال :

ans =
   10
ans =
   37

ans =

کدهای فوق را در Octave بررسی می کنیم:

مثال :

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;

g = differentiate(y,x)

roots([6, 6, -12])

subs(y, x, 1), subs(y, x, -2)

نتیجه :

مثال :

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

ans =

10.0

ans =

37.0-4.6734207789940138748E-18*I

بنابراین، حداقل و حداکثر مقادیر در تابع f (x) = 2×3 + 3×2 – 12x + 17، در بازه ی [-۲،۲] ۱۰ و ۳۷ قرار می گیرد.

حل معادلات دیفرانسیل

متلب تابع dsolve را برای حل معادلات دیفرانسیل ارائه می دهد:

فرم اصلی استفاده از تابع dsolve بصورت زیر است:

مثال :

dsolve('eqn')

1	dsolve('eqn')

این یک راه حل نمادین را با مجموعه ای از ثابت های دلخواه باز می کند.

شما همچنین می توانید شرایط اولیه و مرزی برای مشکل را به عنوان لیست جدا شده با کاما پس از معادله مشخص کنید.

مثال :

dsolve('eqn','cond1', 'cond2',…)

1	dsolve('eqn','cond1', 'cond2',…)

برای این منظور از دستور dsolve استفاده کنید.

برای مثال مشتق (f'(t) = -2*f + cost(t به صورت (‘Df = -2*f + cos(t’ وارد می شود.

مشتقات بالاتر با توجه به D به ترتیب مشتق نشان داده شده است.

برای مثال تابع f”(x) + 2f'(x) = 5sin3x باید بصورت (‘D2y + 2Dy = 5*sin(3*x’ وارد شود.

برای نمونه یک نمونه ساده از یک معادله دیفرانسیل اول مرتب می کنیم: y ‘= 5y

مثال :

s = dsolve('Dy = 5*y')

1	s = dsolve('Dy = 5*y')

نتیجه ی اجرای کد فوق در متلب:

مثال :

s =
   C2*exp(5*t)

1 2	s = C2exp(5t)

مثال ۲ – حل دیفرانسیل y” – y = 0, y(0) = -1, y'(0) = 2:

مثال :

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

1	dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

نتیجه ی احرای کد فوق در متلب :

مثال :

ans =
   exp(t)/2 - (3*exp(-t))/2

1 2	ans = exp(t)/2 - (3*exp(-t))/2

کلام آخر

همانطور که اشاره کردیم یکی از قابلیت های ویژه ی نرم افزار مهندسی متلب ، قابلیت حل انواع معادلات دیفرانسیل در متلب می باشد. از این رو مباحث این بخش را نیز به آموزش حل دیفرانسیل در متلب اختصاص دادیم.

QR: جلسه ۲۲ : حل معادلات دیفرانسیل در متلب

به اشتراک بگذارید

آموزش matlab ,آموزش متلب پیشرفته ,آموزش متلب مقدماتی ,حل معادلات دیفرانسیل در متلب ,دوره کامل آموزش متلب ,محاسبه مشتقات مرتبه بالاتر

دیدگاه کاربران

تعداد دیدگاه : 0

پی وی لرن – آموزش برنامه نویسی و طراحی وب سایت

دوره های آموزشی آکادمی پی وی لرن (پروژه محور و ویژه بازار کار)

جلسه ۲۲ : حل معادلات دیفرانسیل در متلب

مقدمه

حل معادلات دیفرانسیل در متلب

تایید قوانین ابتدایی تمایز

قانون ۱

قانون ۲

قانون ۳

قانون ۴

قانون ۵

قانون ۶

مشتقات توابع نمایشی، لگاریتمی و مثلثاتی

محاسبه مشتقات مرتبه بالاتر

یافتن حداکثر و حداقل یک منحنی

حل معادلات دیفرانسیل

کلام آخر

لیست مطالب دوره

آموزش های پیشرفته

مطالب ویژه

دسته های اصلی

برگه ها

بلاگ